Usean jakauman vertaileminen

Jakaumien kuvaaminen oli viime vuoden lopulla jo aiheena kahdessa kolumnissa, mutta aihe ei tullut vielä loppuun käsitellyksi. Histogrammit, joita aikaisemmat jutut käsittelivät, soveltuvat vain yhden tai kahden jakauman saman aikaiseen esittämiseen. Käytännössä kuitenkin useammin taitaa olla käsillä tilanne, jossa vertailtavana on useampia jatkuva-arvoisia muuttujia eli pitäisi pystyä esittämään isompaa jakaumamäärää.

Pylväskuvioissa on yksi alatyyppi, jonka on suunniteltu usean jakauman samanaikaiseen esittämiseen, nimittäin vaihteluvälikuvio. Vaihteluvälikuvion ajatuksena on esittää pylväillä se alue, jolla muuttujan pienin tai suurin arvo ovat. Usein pylväisiin merkitään lisäksi keskiarvo tai mediaani. Vaihteluvälikuvioissa on useita muunnoksia.

Esimerkiksi kuviossa 1 on vaihteluvälikuvio, jossa pylväät ovat pystysuorassa ja kuviossa 2 pylväät ovat vaakasuorassa. Yleensä tällaisia kuvioita tehdään siten, että se esittää vain yhtä luokkaa. Oheisissa esimerkeissä kuitenkin kysymys on pylväsryhmistä eli ne esittävät useampia luokkia.

Kuvio 1.

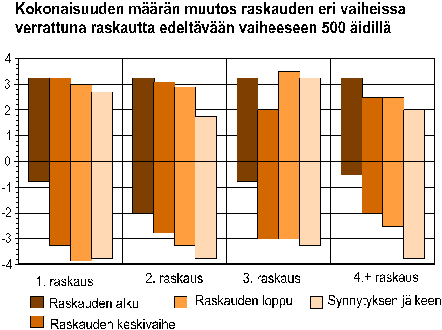
Kuvio 2.

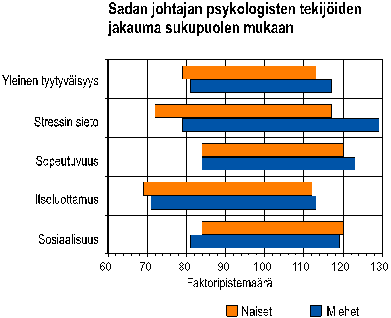
Vaihteluvälikuviot poikkeavat kelluvista pystypylväistä ja liukuvista vaakapylväistä esittämänsä asian kautta: jälkimmäisissä pylväät esittävät - pylväskuvioiden tapaan - määrää, mutta vaihteluvälikuvio sitä lukualuetta, jolla muuttujan arvot ovat.

Kuvioiden 1 ja 2 suurin ongelma on, että ne eivät kuvaa jakaumaa kovin tarkasti. Usein parempi esitys syntyy siten, että pylväiden ääripäät jätetään pois eli pienimmän ja suurimman arvon sijasta käytetään esimerkiksi neljännespisteitä eli kvartiileja. Tällöin siis kuvataan sitä, mille kohtaa sijoittuu jakauman keskiosa, koska 25 % sekä pienimmistä että suurimmista havainnoista on jätetty pois. Neljännespisteiden sijasta voidaan luonnollisesti käyttää myös muita niin sanottuja fraktiileja, esimerkiksi kymmenyspisteitä.

Jakaumien kuvaamisessa kenties paras vaihtoehto kuitenkin on niin sanottu laatikko ja viikset -esitys, jota olen joskus aikaisemminkin käsitellyt tällä palstalla (Tietoaika 7/92). Tämän kuviotyypin englanninkieliset nimitykset ovat joko box plot tai box and wiskers.

Kuviossa 3 on laatikko ja viikset -esitys samoista muuttujista, jotka ovat kuviossa 2. Tässä kuviotyypissä laatikko on neljännespisteiden välinen osa eli siihen väliin sijoittuu 50 % havainnoista. Kummassakin päässä oleva "viiksi" ulottuu pienimpään ja suurimpaan havaintoon. Laatikon sisälle merkitään useimmiten mediaani, joka kuviossa 3 on esitetty viivalla. Lisäksi laatikon sisällä oleva kärki osoittaa keskiarvon. Näiden merkintöjen kautta saa selvästi paremman käsityksen jakauman luonteesta kuin kuviosta 1 - edellyttäen, että jakaumat ylipäätään ovat tuttuja.

Kuvio 3.

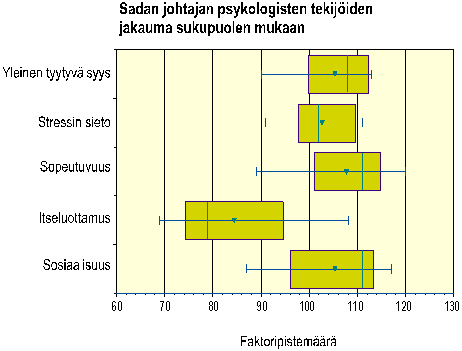
Kuvio 4.

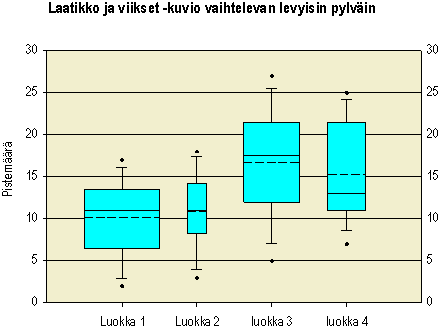
Kuviossa 4 on vielä vähän lisätty versio laatikko ja viikset -esityksestä. Siinä laatikot ovat eri levyisiä ja laatikon leveys on suhteessa siihen sisältyvien havaintojen määrään eli leveiden laatikkojen takana on enemmän havaintoja kuin kapeiden. Näin menetellään usein tieteellisissä esityksissä, joissa havaintojen määrä on keskeinen ominaisuus.

Jakaumaa esittävien kuvioiden käyttö ei ole kovin tavallista. Syynä on osittain se, että esitystavat eivät ole tuttuja. Osittain syynä kuitenkin lienee se, että käsitteellisesti jakaumat ja niiden merkitys eivät ole tuttuja, ja jakauma tiivistetään yhdeksi luvuksi, esimerkiksi keskiarvoksi.

Päivitetty 14.2.2002

Lisätietoja:
sähköposti: tietoaika@tilastokeskus.fi