Julkaistu: 13.3.2002
Gini ja tuloerot
Tuloeroja mitataan Gini-kertoimella. Kertoimella ei ole mitään tekemistä alkoholin kanssa, vaan nimi on laskentamenetelmän kehittäjän nimi. Kun kerrointa yleensä käytetään, sen laskutapa sivuutetaan ilma selostusta, koska kerrointa pidetään monimutkaisena. Kertoimen perusidean ymmärtäminen ei kuitenkaan ole pahaksi tuloerojen pohdinnassa.
Edellisessä tekstissäni selvitin hajontalukujen, lähinnä varianssin ja keskihajonnan, perusideaa. Myös Gini-kerroin on hajontaluku. Viime kuukauden jutussa hajontaa laskettiin vertaamalla kaikkia havaintoja keskiarvoon. Keskihajonta kertoo, miten kaukana keskiarvosta jakauman havainnot keskimäärin ovat.
Gini-kerroin taas vertaa jakauman kaikkia havaintoja keskenään. Gini-kertoimen perusideana on laskea, miten kaukana keskimäärin jakauman havainnot ovat toisistaan.
Yksinkertaistaen siis lasketaan ensin, mikä on yhden yksikön keskimääräinen etäisyys kaikista jakauman yksiköistä. Toistetaan kaikkien yksiköiden kohdalla sama operaatio ja lasketaan lopuksi em. keskimääräisten etäisyyksien keskiarvo. Koska on tarpeen saada tunnusluku, joka kuvaa tuloeroja riippumatta tulotasosta, skaalataan saatu tunnusluku jakauman keskiarvon avulla. Saatu luku vaihtelee nollan ja ykkösen välillä riippumatta siitä, mikä on tulotaso.
Gini-kerroin saa maksimiarvon 1 silloin, kun kaikki tulot ovat keskittyneet yhdelle yksikölle. Arvo 0 taas saadaan tilanteessa, jossa tulot ovat jakautuneet tasan.
Gini-kertoimen varsinainen laskukaava on hieman monimutkaisempi, kuten oheinen esimerkki osoittaa.
Tuloeroja kuvataan myös varianssin/keskihajonnan avulla skaalamalla tunnusluku keskiarvolla. Gini-kerroin on kuitenkin vakaampi mittari tulonjaon tyyppisissä jakaumissa, jotka ovat vinoja (jakauman yläpää jatkuu paljon kauemmaksi keskiarvosta kuin alapää). Se reagoi varsinaisia hajontalukuja vaimeammin jakauman yläpäässä tapahtuviin muutoksiin.
Esimerkki Gini-kertoimen laskemisesta
Gini-kertoimen laskukaava: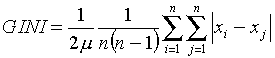
![]() = keskiarvo
= keskiarvo
n =havaintojen lukumäärä
xi,j = havaintojen arvot
Oletetaan, että tutkittavanamme on vain kolme yksilöä, Maija, Ville ja Kalle. Oletetaan, että Maijalla on varallisuutta 2 000 euroa, Villellä 5 000 euroa ja Kallella 3 000 euroa. Heillä on varallisuutta keskimäärin 3 333,33 euroa. Maijan varallisuus poikkeaa jakauman havaintojen varallisuudesta keskimäärin 1 333 eurolla, Villen 1 666 eurolla ja Kallen 1 000 eurolla. Kun arvot sijoitetaan kaavaan, saadaan Gini-kertoimen arvoksi 0,30.
Jos Maijan, Villen ja Kallen varallisuus olisi kaikilla sama, esim. 3 000 euroa, olisi kunkin havainnon poikkeama muista havainnoista keskimäärin 0 euroa. Em. kaavaan sijoitettuna nämä arvot tuottavat Gini-kertoimen arvoksi 0.
Jos taas koko 10 000 euron varallisuus olisi Villellä, olisi kunkin keskimääräinen poikkeama 3 333,33 euroa. Kaavaan sijoittelun jälkeen tuloksena olisi Gini-kerroin 1.
Jussi Melkas
- Ginikertoimen kuvaus pohjautuu Veli-Matti Törmälehdon kuvaukseen ja esimerkki Sanna Rajakankaan laatimaan esimerkkiin.
Päivitetty 13.3.2002
Lisätietoja:sähköposti: tietoaika@tilastokeskus.fi

