Julkaistu: 9.4.2002
Parven ymmärtäminen
Ihmisen kykyä tulkita ja ymmärtää visuaalisia viestejä on tutkittu erittäin paljon ja monelta kantilta. En tarkoita pelkästään tilastografiikkaa, vaan laajemmin visuaalisten esitysten ymmärtämistä. Tällaisten viestien tulkinta on monimutkainen prosessi eikä sitä tunneta kaikilta osin. Keskeinen vaatimus on, että kaikki ymmärtävät viestin samalla tavalla. Olisi tuhoisaa, jos esimerkiksi liikennemerkkien viestit tulkittaisiin eri tavoin. Useimmissa tilanteissa visuaalisten viestien ymmärtämistä voidaan tutkia luotettavasti vain järjestämällä kokeita. Tilastografiikka ei ole poikkeus.
Mosteller työtovereineen (Mosteller,F., Siegel, A. F., Trapido E., Youtz C.: Eye fitting stragiht lines. The American Statistician, 1981,35,3) teki pienimuotoisen kokeen, jonka aiheena oli, kuinka satakunta opiskelijaa ja tutkijaa sijoittivat suoran viivan pisteparven päälle kuvaamaan pisteparveen sisältyvää riippuvuutta. Kuviossa 1 ovat ne neljä parvikuviota, joita testissä käytettiin. Sijoitettava viiva oli läpinäkyvällä kalvolla ja se piti sijoittaa silmämääräisesti pisteiden päälle niin kuin se parhaiten tuntui sopivan.
Kuvio 1
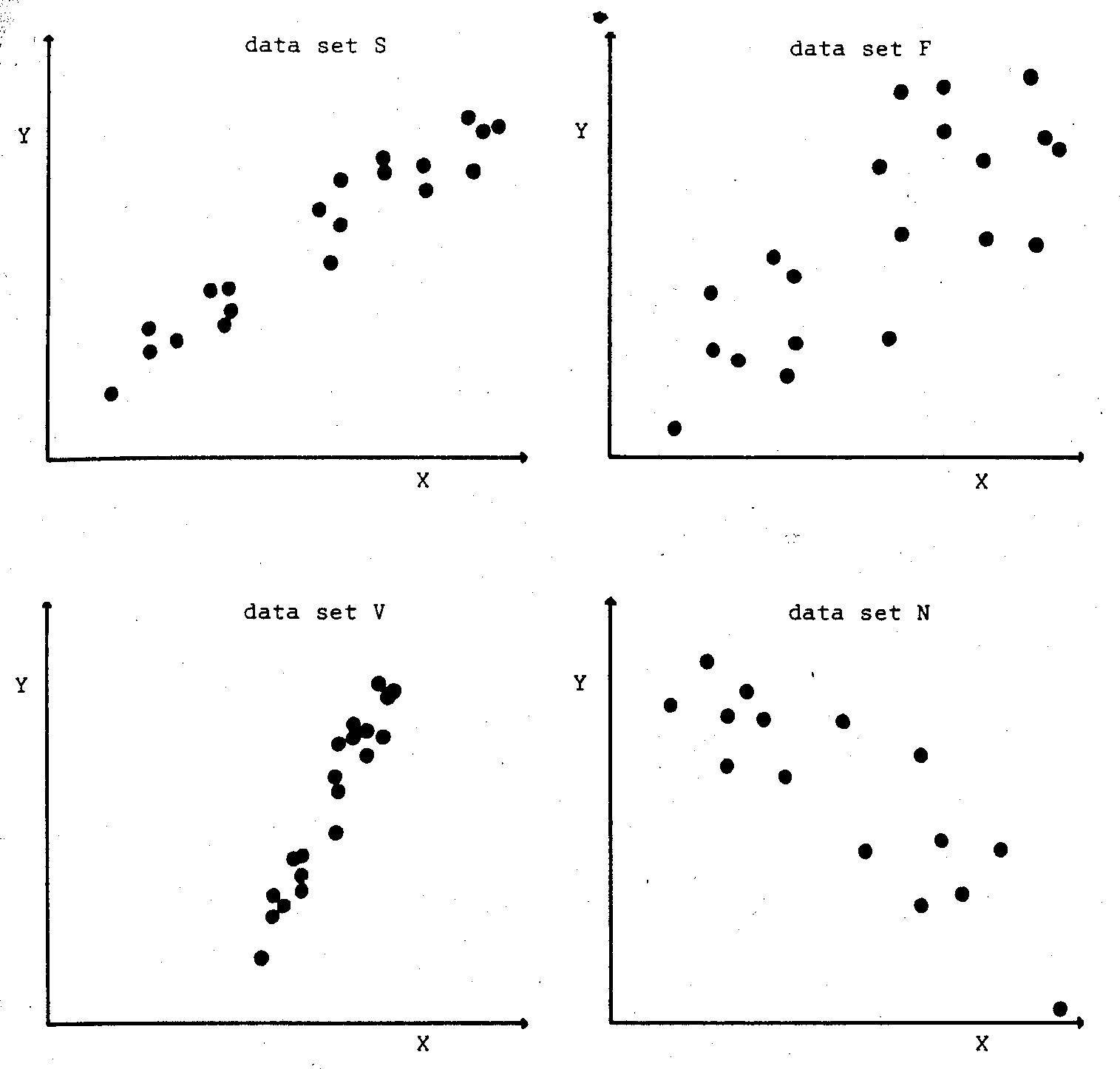
Tilastotieteen keinoin voidaan laskea niin sanottu regressiosuora kuvaamaan muuttujien välistä riippuvuutta. Monissa yhteyksissä regressiosuora on paljon yleisemmin käytetty kuin parvikuvio ja siksi on kiinnostavaa, kuinka hyvin matemaattinen esitys vastaa sitä intuitiivista käsitystä, joka parvikuviosta syntyy. Kuviossa 2 on kuvion 1 F -paneelin pisteet ja niiden päälle piirretty luvuista laskettu regressiosuora. Regressiosuoran voi karkeasti ajatella sijoittuvan pisteparven keskelle siten, että kaikista pisteistä pystysuoraan viivalle piirrettyjen janojen yhteispituus on pienin mahdollinen. Regressiosuora kulkee aina pisteparven painopisteen kautta ja on siis eräänlainen tasapainosuora.
Kuvio 2 Kuvion 1 paneelin F parvikuvio ja sen pisteistä laskettu regressiosuora
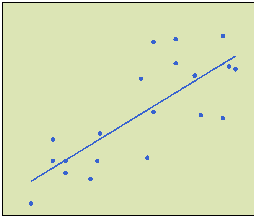
Kokeen tarkoituksena oli selvittää toisaalta sitä, kuinka hyvin regressiosuora vastaa ihmisten intuitiota riippuvuuden laadusta ja toisaalta sitä, kuinka paljon ihmisten arviot suoran paikasta vaihtelivat. On huomattava, että tutkijoille ajatus regressiosuorasta oli tuttu, mutta opiskelijat eivät olleet perehtyneet tilastotieteeseen ennen koetta.
Tulos oli, että opiskelijoiden sijoittamat suorat olivat hyvin lähellä laskettuja suoria kaikissa muissa paneeleissa paitsi F:ssä. Kokeen tekijät selittivät tämän johtuvan siitä, että opiskelijat sijoittivat suoran niin sanotun pääkomponentin eli pisteparven pääakselin suuntaisena. Se eroaa regressiosuorasta siten, että etäisyys lasketaan kohtisuoraan viivaa kohti eikä pystysuoraan. Tutkijat, joille regressiosuora oli tutumpi, sijoittivat viivan hyvin lähelle regressiosuoraa.
Toinen havainto oli, että ne jotka asettivat viivan yhteen kuvioon "liian" jyrkästi olivat taipuvaisia tekemään niin kaikkien kuvioiden kohdalla (tosin erot eivät olleet kovin suuria). Toisin sanoen, tapa nähdä pisteparven muoto ja arvioida siihen sisältyvä riippuvuus on osittain henkilökohtainen, ei siis täysin universaali, ominaisuus.
Tällainenkin pieni koe osoittaa, että ainakin parvikuvioiden sanoma ymmärretään suhteellisen samalla tavalla ja myös "oikein". Tosin vaihteluakin siinä on. Kuvion 1 eri paneeleja vertailtaessa huomaa, että paneelin F pisteparven hajonta on suurempi kuin muissa paneeleissa. Tämän paneelin kohdalla myös arviot vaihtelivat eniten. Tästä voidaan tehdä johtopäätös, että jos kuvion sanoma on hajanainen, diffuusi, myös sen sanoman tulkinnassa esiintyy vaihtelua. Yhtenäisen, koherentin, kuvion tulkinta taas on yhtenäisempää.
Päivitetty 9.4.2002
Lisätietoja:sähköposti: tietoaika@tilastokeskus.fi

