Karttojen moninaiset luokat

Tilastotieteilijänä minulle oli itsestään selvää, että jakaumaa kuvattaessa jakauman todellinen luonne, "muoto", tuli säilyttää kaikissa tilanteissa. Luokitusta tehtäessä pyrkimyksenä on sellainen luokkajako, jossa jakaumasta tulee oikean muotoinen ja siinä ei ole satunnaisvaihtelun tuomaa kohinaa (vrt. Tietoaika 12/2001). Niinpä olinkin kuin klapilla päähän lyöty, kun aloin selvitellä, millaisia ohjeita jakaumien käsittelyyn annetaan teemakarttojen, erityisesti koropleettikarttojen, yhteydessä.

Teemakarttojen laatijoille edellä mainittu lähestymistapa tuntuu olevan vain yksi mahdollisuus muiden joukossa. Esimerkiksi tunnetussa kartografian oppikirjassa (Kraak ja Ormeling: Cartography; Visualisation of Spatial Data. Addison Wesley Longman, 1996) esitellään viisi muuta luokitteluperiaatetta. Luokittelu, josta olen aikaisemmin puhunut perustui siihen, että luokkien määrä lasketaan havaintojen määrästä ja luokkien välit ovat aina samoja. Kaavamaisesti luokkavälit voitaisiin esittää (hieman epätäsmällisesti) seuraavana sarjana: minimi + L + L + L + L (= suurin arvo). Kyseisessä kirjassa mainitaan myös tämä tasavälinen menetelmä, mutta luokkien maksimimääräksi asetetaan seitsemän, koska sen enempää luokkia ihmiset eivät pysty hahmottamaan.

Toinen tavanomainen menetelmä perustui kvartiileihin (tai kvantiileihin). Siinä luokkarajoiksi otetaan alakvartiili, mediaani ja yläkvartiili. Kvartiilien sijasta voidaan luonnollisesti käyttää kvantiileja.

Aritmeettisen sarjan tapaan muodostettuina luokkavälit, kun lasketaan viisi luokkaa ovat seuraavat: minimi + L + 2L +3L + 4L + 5L (= suurin arvo). Tässä tapauksessa luokkavälit kasvavat tasaisesti.

Geometrisen sarjan tapaan luokkarajat (ja luokkavälit) määrätään kertomalla edellinen arvo määrätyllä vakiolla C. C (oikeastaan C:n logaritmi) saadaan jakamalla pienimmän ja suurimman arvon logaritmi luokkien lukumäärällä. Luokkarajat saadaan sitten seuraavalla algoritmilla: logaritmi suurimmasta arvosta - C = logaritmi toiseksi suurimmasta arvosta; logaritmi toiseksi suurimmasta arvosta - C = logaritmi kolmanneksi suurimmasta arvosta; jne. Kun sitten otetaan antilogaritmit saaduista arvoista, saadaan luokkarajat.

Harmoniset luokkarajat saadaan geometristen tapaan, kun logaritmi korvataan käänteisarvolla. Toisin sanoen vakion C käänteisarvo (eli 1/C) saadaan jakamalla suurimman arvon käänteisarvon ja pienimmän arvon käänteisarvon erotus luokkien lukumäärällä. Luokkarajat saadaan vastaavalla algoritmilla kuin geometrisessa sarjassakin, kun logaritmi korvataan käänteisarvolla. Tämä menettely tuottaa tarkan jaon pienille arvoille, ja jako harvenee isompiin arvoihin edettäessä.

Sisäkkäisessä luokkajaossa lasketaan ensin arvojen keskiarvo. Sitten jatketaan laskemalla uudet keskiarvot erikseen edellistä keskiarvoa pienemmistä havainnoista ja suuremmista havainnoista. Algoritmi jatkuu niin, että kunkin luokkavälin arvoista lasketaan jälleen keskiarvot, kunnes saadaan haluttu määrä luokkia. Näin päädytään aina parilliseen luokkien määrään.

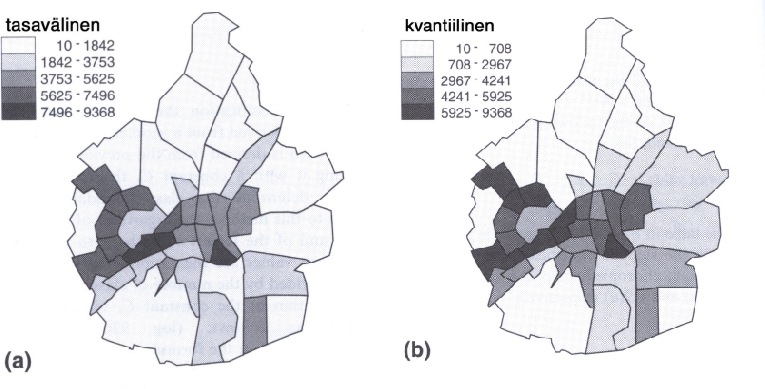
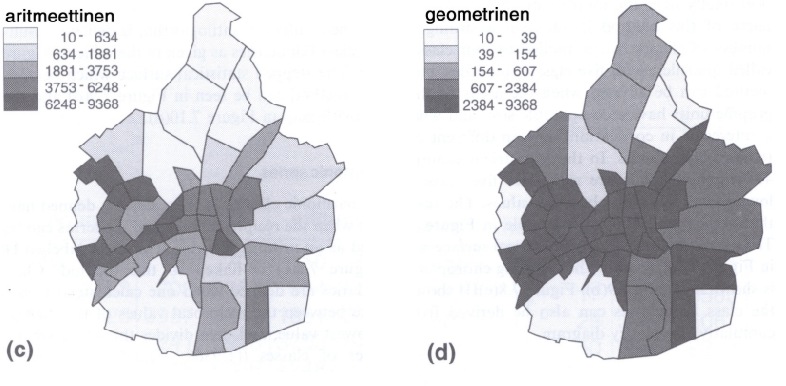
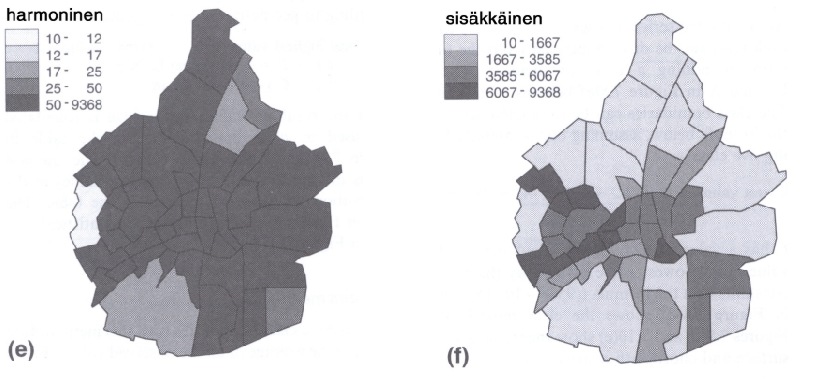
Oheisessa kuviossa, joka on kopioitu Kraakin ja Ormelingin kirjasta, nähdään miten erilaisiin koropleettikarttoihin erilaisilla luokkajoilla päädytään. Se mikä minua tässä tilastotieteilijänä kummastuttaa on, että missään ei ole annettu objektiivisia kriteereitä, milloin mitäkin luokitusta pitäisi käyttää. Tulos saattaa näyttää varsin erilaiselta eri luokituksilla, ja ellei kriteerejä ole, voi teemakartan laatija valita haluamansa omien mieltymystensä tai tavoitteidensa mukaan. Sellainen asiantila ei ole millään muotoa toivottava. Kenties joku maantieteilijä osaa opastaa minua (ja muita) tässä asiassa.

Päivitetty 1.7.2002

Lisätietoja:
sähköposti: tietoaika@tilastokeskus.fi