Julkaistu: 15.10.2002
Valekerroin
Pylväskuviot, joissa määräasteikko on katkaistu eivät ole nykyisin kovin tavallisia, mutta joskus sellaisiakin kuvioita vielä näkee. Kuviossa 1 on esimerkki Iltalehdestä. Siinä kuvataan lehden levikin muutosta viime vuosien ajalta. Nopeasti katsoen näyttäisi siltä, että levikki on yli kaksinkertaistunut vuodesta 1997 vuoteen 2001, mutta todellisuudessa lisäys on ollut 20 %. Vaikutelma johtuu siitä, että määräasteikon voidaan katsoa alkavan 100 000:sta.
Kuvio 1.
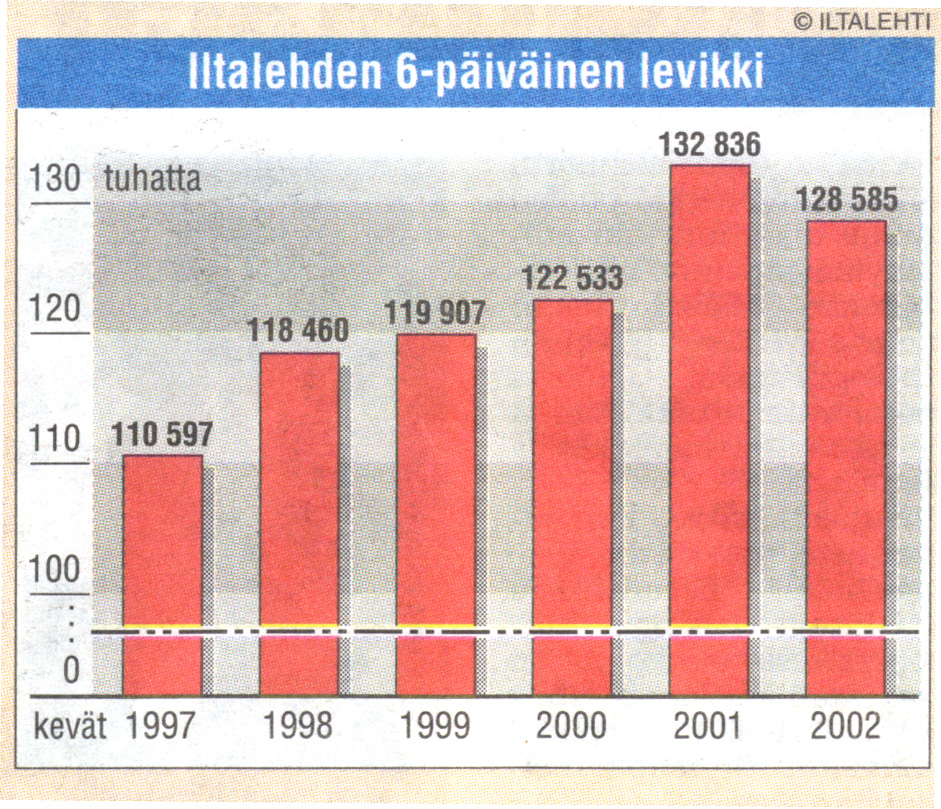
Kuten olen useasti aikaisemmin todennut, valekertoimen arvo nousee väistämättä, jos pylväskuvioiden määräasteikkoa typistetään. Valekerroin tai havaintovääristymäkerroin kuvaa sitä, kuinka paljon kuvio liioittelee muutosta tai laajemmin ajatellen ilmiön piirteitä. Silloin kun valekertoimen arvo on 1, kuvio esittää ilmiön todellisuutta vastaavasti.
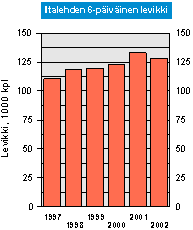
Kuvio 2 on sama esitys kuin kuvio 1, mutta ilman, että määräasteikkoa olisi katkaistu, ja siinä valekerroin saa siis arvon 1. Niinpä siitä näkeekin välittömästi, että kasvu vuodesta 1997 vuoteen 2001 oli viidenneksen luokkaa.
Kuvio 2.
Kuvion 1 valekerroin sen sijaan on 6,2. Se saadaan seuraavasti: Ensin lasketaan, kuinka monta prosenttia muutos todellisuudessa oli pienimmästä arvosta suurimpaan eli (132 836-110 597)/110 597 = 0,201 eli 20,1 %. Sitten mitataan vastaavien pylväiden pituudet (alkuperäisestä kuviosta) ja suoritetaan samat laskutoimitukset (4,5-2,0)/2,0 = 1,25 jolloin muutos on 125 %. Valekerroin saadaan lopuksi jakolaskusta 125/20,1 ja tulos on siis 6,2.
Valekertoimen kasvu johtuu siitä, että kun eri mittaisista pylväistä katkaistaan saman kokoinen pala, niistä itse asiassa poistetaan suhteellisesti eri suuruinen osa. Esimerkiksi kuviossa 1 pisimmästä pylväästä puuttuu noin 60 %, mutta lyhyimmästä pylväästä selvästi yli 70 %. Mitä suurempi tämä ero on, sitä suuremmaksi valekerroin muodostuu.(Jos kaikki pylväät olisivat saman mittaisia, valekertoimen arvo pysyisi ykkösenä riippumatta poistetun osan koosta.)
Kuviosta 1 voidaan laskea useita valekertoimia, mutta yleisin tapa on laskea se isoimman ja pienimmän alkion välille. Valekertoimen laskemisessa on tiettyä epämääräisyyttä ja sitä voidaan pitää osittain vitsinä, mutta sitä se ei ole. Kokeellisesti on nimittäin pystytty osoittamaan, että se kuvaa suhteellisen tarkasti sitä, miten (väärin) kuvio tulkitaan.
Pylväskuvio, jossa määräasteikkoa on typistetty, on eräässä mielessä rinnastettavissa taulukkoon. Esitys sellaisenaan ei välitä (oikeaa) visuaalista viestiä. Asioiden tila pitää selvittää mielessään lukujen avulla samoin kuin taulukossakin. Toisaalta kuitenkin on huomattava, että taulukosta virheellisten johtopäätösten tekeminen on epätodennäköistä. Kuvion 1 kohdalla tällainen vaara on ilmeinen.
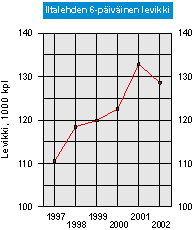
On huomattava, että viivakuvion kohdalla tilanne on toisenlainen. Pylväskuvioissa määrällistä informaatiota kantaa pinta-ala. Koska pylväät ovat yleensä saman levyisiä, pylväiden pituuden ja pinta-alan välillä on yksi yhteen -vastaavuus. Viivakuviossa pinta-alalla on vähäisempi merkitys. Se mikä viivakuviossa ensimmäiseksi huomataan, on viivan profiili eli kehityssuunta (trendi) ja vaihtelu. Niinpä viivakuviossa määräasteikon typistäminen ei aiheuta samanlaista harhaa kuin pylväskuvioissa. Viivakuvio voidaan tehdä siis kuten kuvio 3, jos halutaan kuvata vain trendiä ja vaihtelua trendin suhteen. Jos tarkoitus on kuvata suhteellista trendiä, silloin myös viivakuviossa määräasteikon on alettava nollasta.
Kuvio 3.
Päivitetty 15.10.2002
Lisätietoja:sähköposti: tietoaika@tilastokeskus.fi

